6.1. Linear Regression¶
6.1.1. Co to jest Linear Regression?¶
The straight line can be seen in the plot, showing how linear regression attempts to draw a straight line that will best minimize the residual sum of squares between the observed responses in the dataset, and the responses predicted by the linear approximation.
The coefficients, the residual sum of squares and the variance score are also calculated.
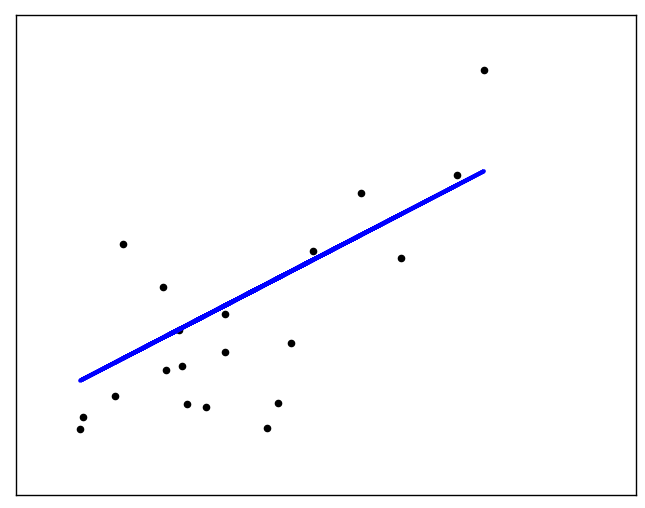
Figure 6.6. The straight line can be seen in the plot, showing how linear regression attempts to draw a straight line that will best minimize the residual sum of squares between the observed responses in the dataset, and the responses predicted by the linear approximation.¶
6.1.2. Przed zastosowaniem¶
Trzeba usunąć elementy odstające
Trzeba sprawdzić czy są osobne klastry danych, tzn. czy linia jest przedziałami ciągła, tzn. gdyby podzielić na segmenty, to można lepiej dostosować regresję
6.1.3. Wyznaczanie równania prostej¶
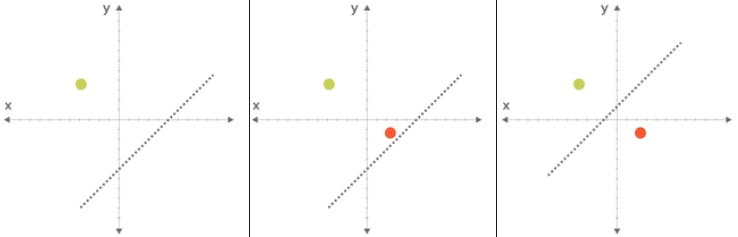
Figure 6.7. Manipulowanie parametrami prostej (klasyfikatora) w celu określenia funkcji.¶
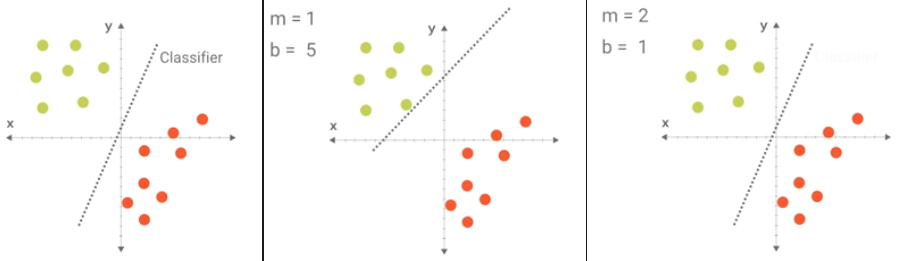
Figure 6.8. Wyznaczanie równania prostej.¶
6.1.4. Funkcja przedziałami liniowa¶
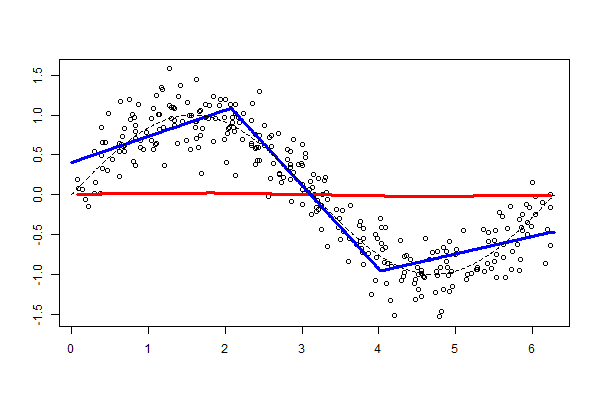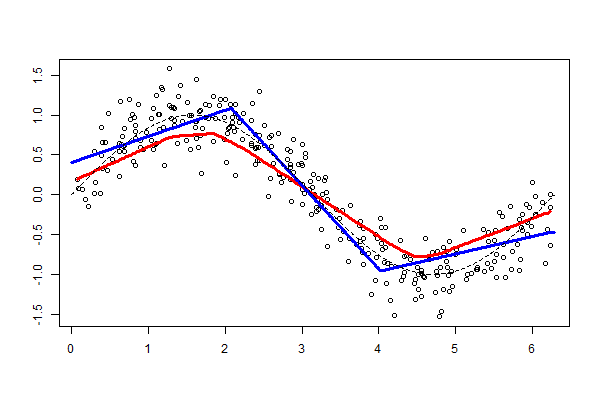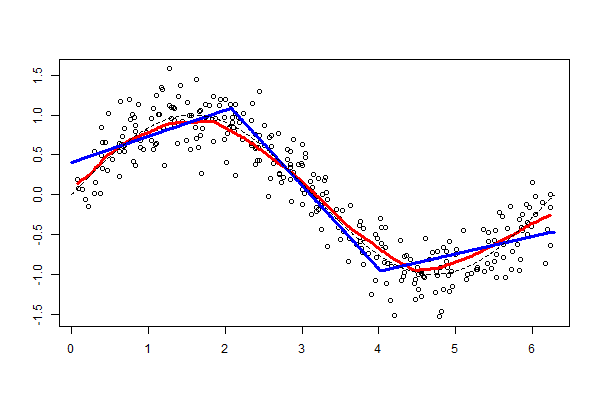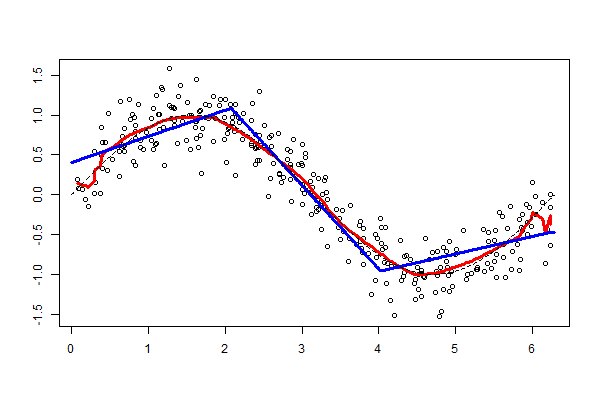
Figure 6.9. Funkcja przedziałami liniowa¶
6.1.5. Przykłady praktyczne¶
Wykorzystanie biblioteki sklearn
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
# Load the diabetes dataset
diabetes = datasets.load_diabetes()
# Use only one feature
diabetes_features = diabetes.data[:, np.newaxis, 2]
# Split the data into training/testing sets
features_train = diabetes_features[:-20]
features_test = diabetes_features[-20:]
# Split the targets into training/testing sets
labels_train = diabetes.target[:-20]
labels_test = diabetes.target[-20:]
# Create linear regression object
model = linear_model.LinearRegression()
# Train the model using the training sets
model.fit(features_train, labels_train)
# The coefficients
print('Coefficients: \n{model.coef_}')
# The mean squared error
print("Mean squared error: %.2f"
% np.mean((model.predict(features_test) - labels_test) ** 2))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % model.score(features_test, labels_test))
# Plot outputs
plt.scatter(features_test, labels_test, color='black')
plt.plot(features_test, model.predict(features_test), color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show() # doctest: +SKIP
Coefficients: [ 938.23786125]
Mean squared error: 2548.07
Variance score: 0.4

Figure 6.10. The straight line can be seen in the plot, showing how linear regression attempts to draw a straight line that will best minimize the residual sum of squares between the observed responses in the dataset, and the responses predicted by the linear approximation.¶
6.1.6. Własna implementacja¶
import pandas as pd
from math import pow
def cal_mean(readings):
"""
Function to calculate the mean value of the input readings
"""
readings_total = sum(readings)
number_of_readings = len(readings)
mean = readings_total / float(number_of_readings)
return mean
def cal_variance(readings):
"""
Calculating the variance of the readings
"""
# To calculate the variance we need the mean value
# Calculating the mean value from the cal_mean function
readings_mean = cal_mean(readings)
# mean difference squared readings
mean_difference_squared_readings = [pow((reading - readings_mean), 2) for reading in readings]
variance = sum(mean_difference_squared_readings)
return variance / float(len(readings) - 1)
def cal_covariance(readings_1, readings_2):
"""
Calculate the covariance between two different list of readings
"""
readings_1_mean = cal_mean(readings_1)
readings_2_mean = cal_mean(readings_2)
readings_size = len(readings_1)
covariance = 0.0
for i in range(0, readings_size):
covariance += (readings_1[i] - readings_1_mean) * (readings_2[i] - readings_2_mean)
return covariance / float(readings_size - 1)
def cal_simple_linear_regression_coefficients(x_readings, y_readings):
"""
Calculating the simple linear regression coefficients (B0, B1)
"""
# Coefficient B1 = covariance of x_readings and y_readings divided by variance of x_readings
# Directly calling the implemented covariance and the variance functions
# To calculate the coefficient B1
b1 = cal_covariance(x_readings, y_readings) / float(cal_variance(x_readings))
# Coefficient B0 = mean of y_readings - ( B1 * the mean of the x_readings )
b0 = cal_mean(y_readings) - (b1 * cal_mean(x_readings))
return b0, b1
def predict_target_value(x, b0, b1):
"""
Calculating the target (y) value using the input x and the coefficients b0, b1
"""
return b0 + b1 * x
def cal_rmse(actual_readings, predicted_readings):
"""
Calculating the root mean square error
"""
square_error_total = 0.0
total_readings = len(actual_readings)
for i in range(0, total_readings):
error = predicted_readings[i] - actual_readings[i]
square_error_total += pow(error, 2)
rmse = square_error_total / float(total_readings)
return rmse
def simple_linear_regression(dataset):
"""
Implementing simple linear regression without using any python library
"""
# Get the dataset header names
dataset_headers = dataframe.columns.values(dataset)
print("Dataset Headers :: ", dataset_headers)
# Calculating the mean of the square feet and the price readings
square_feet_mean = cal_mean(dataset[dataset_headers[0]])
price_mean = cal_mean(dataset[dataset_headers[1]])
square_feet_variance = cal_variance(dataset[dataset_headers[0]])
price_variance = cal_variance(dataset[dataset_headers[1]])
# Calculating the regression
covariance_of_price_and_square_feet = dataset.cov()[dataset_headers[0]][dataset_headers[1]]
w1 = covariance_of_price_and_square_feet / float(square_feet_variance)
w0 = price_mean - (w1 * square_feet_mean)
# Predictions
dataset['Predicted_Price'] = w0 + w1 * dataset[dataset_headers[0]]
if __name__ == "__main__":
input_path = '../_data/input-data.csv'
house_price_dataset = pd.read_csv(input_path)
simple_linear_regression(house_price_dataset)
6.1.7. Assignments¶
6.1.7.1. Least square regression 3 points¶
Assignment: Least square regression 3 points
Complexity: easy
Lines of code: 10 lines
Time: 13 min
- English:
Consider the following set of points: \({(-2 , -1) , (1 , 1) , (3 , 2)}\)
Find the least square regression line for the given data points.
Plot the given points and the regression line in the same rectangular system of axes.
Napisz własny kod implementujący rozwiązanie
Run doctests - all must succeed
- Polish:
6.1.7.2. Least square regression 4 points¶
Assignment: Least square regression 4 points
Complexity: easy
Lines of code: 10 lines
Time: 13 min
- English:
Find the least square regression line for the following set of data: \({(-1 , 0),(0 , 2),(1 , 4),(2 , 5)}\)
Plot the given points and the regression line in the same rectangular system of axes.
Użyj kodu z przykładu własnej implementacji do rozwiązania
Run doctests - all must succeed
- Polish:
6.1.7.3. Company sales¶
Assignment: Company sales
Complexity: easy
Lines of code: 10 lines
Time: 13 min
- English:
The sales of a company (in million dollars) for each year are shown in the table below.
x (year) 2005 2006 2007 2008 2009 y (sales) 12 19 29 37 45
Find the least square regression line \(y = ax + b\) .
Use the least squares regression line as a model to estimate the sales of the company in 2012.
Use
sklearnRun doctests - all must succeed
- Polish: